Prediction of Enzyme Thermal Stability by Computational Methods
Koichi Tamura
(Research and Development Department)
Introduction
Enzymes are biopolymers (mainly proteins) that catalyze a wide variety of chemical reactions. Due to their lower environmental impact and high selectivity compared to metal catalysts, enzymes are widely used in industrial, food, and other applications. In general, the rate of chemical reactions depends on temperature; as the temperature increases, the reaction rate also rises. This is because heating provides the energy needed to overcome the reaction's activation barrier. For example, the Haber-Bosch process, which synthesizes ammonia from nitrogen and hydrogen using inorganic iron-based catalysts, operates at temperatures approaching 500°C.
In contrast, enzymes, being biopolymers, cannot withstand such extreme conditions and unfold (denature) at a certain temperature. This temperature is referred to as the melting temperature (Tm). Tm is a critical indicator for assessing an enzyme's thermal stability, and predicting and improving Tm is a key challenge in protein engineering. At digzyme, we have developed a computational method to predict scores correlated with enzyme Tm, enabling the selection of enzymes that function at high temperatures and the improvement of enzyme performance to meet a broader range of needs.
In this blog, we evaluate the performance of our developed method using two datasets of experimentally derived protein thermal stability data.
Methodology
In the context of enzyme discovery and modification, target enzymes for thermal stability prediction often originate from a wide variety of species and protein families. Therefore, prediction models require versatility, independent of these two factors. To meet this requirement, various methods have been proposed, which can be broadly categorized into the following two approaches:
1. Data-Driven Approaches
This approach, often referred to as machine learning, involves constructing predictive models for protein thermal stability based on large datasets derived from experimental results. The process of building these models is called training. The duration of training depends on the amount of data and the complexity of the model, ranging from the time it takes to enjoy a cup of coffee to an entire week of computation using cutting-edge GPGPU (General-Purpose Graphics Processing Unit) systems. Once a trained model is established, the computational cost for subsequent predictions is significantly lower than during the training phase.
As suggested by the model construction process, the accuracy of machine learning models heavily depends on the quantity and quality of the training data. Limited data introduces bias into the inferred rules, and care must also be taken to ensure the training data is not skewed toward specific species or protein families. Additionally, consistent experimental conditions for measuring protein properties are desirable, although achieving this is challenging given that data in current databases originates from various research groups.
Even with attention to data quantity and bias, generalizability issues may persist, primarily due to overfitting and extrapolation challenges. Overfitting occurs when a machine learning model overly adapts to the training data, yielding excellent predictions for the training set but failing with new data. Preventing overfitting requires expert techniques, such as appropriately controlling model complexity. Extrapolation refers to the model's ability to maintain reliability for data outside the training range. For proteins, this means being able to make reliable predictions for novel amino acid sequences with low homology to the training data. This capability is critical in enzyme discovery and modification because the target sequences often show low similarity to previously studied enzymes. While extrapolation is a crucial feature, building models inherently equipped with it is difficult except for simple linear models. Thus, the best practice here is to thoroughly understand and respect the applicability domain of the constructed machine learning models.
2. Physics-Based Approaches
Physics-based models begin by constructing energy functions that describe atomic interactions. The universal natural laws governing atomic and molecular systems have been mathematically formulated for over a century. Simple examples allow manual solutions to these equations, enabling comparison with experimental values to validate their accuracy (see introductory physical chemistry textbooks for details). Since these equations include no arbitrary parameters apart from physical constants (e.g., the speed of light, Planck's constant), they offer universal applicability. However, for complex multi-atomic systems like enzymes in solvents, these equations become highly intricate, making their practical computation infeasible even with state-of-the-art computational resources.
To address this, approximations are introduced to simplify the equations, trading off precision and universality for computational feasibility. Common approximation methods include:
●Empirical Energy Functions in Molecular Mechanics: These functions simplify inherently complex atomic interactions by assuming basic functional forms and introducing parameter sets.
●Treatment of Solvents via Statistical Mechanics: Instead of explicitly modeling numerous solvent molecules around the enzyme, their effects are replaced with averaged quantities.
These approximations significantly reduce computational costs but at the expense of accuracy and universality.
digzyme Score
At digzyme, we adopt a physics-based approach to predict enzyme thermal stability. Our model takes three-dimensional structural information of enzymes as input and outputs a score—referred to as the "digzyme score." This score is designed to correlate with the enzyme's melting temperature (Tm) and typically falls near a value of 1.0. While it does not directly predict the exact Tm value, this design suffices for practical purposes, such as comparing the relative stability of multiple enzymes.
Case Study 1: Prediction of Mutant Thermal Stability
In order to computationally design and select useful enzyme mutants, it is necessary to calculate various properties of numerous candidate mutants and rank them based on their values. Among these properties, thermal stability is particularly important. Below, we compare the results of multiple groups and digzyme in a competition to predict the difference in unfolding free energy (ΔΔGu) between the wild-type and mutants of frataxin, an enzyme involved in iron-sulfur cluster regeneration.
A competition was held in 2018 to predict the difference in unfolding free energy (ΔΔGu) between the wild-type and eight mutants of frataxin[1], and the results were published in a paper in 2019[2]. Unfolding free energy (ΔGu) is defined by the equation (1), where...
ΔGu = Gu - Gf (1)
It is defined as the change in free energy associated with the unfolding of the enzyme. Here, Gu and Gf represent the free energies of the unfolded and folded states, respectively. In general, since the folded state of the enzyme is more stable, ΔGu is greater than 0. Note that the larger the ΔGu, the more difficult it is for the enzyme to unfold (i.e., the more stable it is). For both the wild-type and mutant forms, the unfolding free energy defined by equation (1) is measured, and by calculating the difference between them, the change in unfolding free energy due to the mutation can be computed as follows:
ΔΔGu = ΔGu(mutant) - ΔGu(wild-type) (2)
ΔΔGu < 0 Then, it means that the enzyme has become destabilized due to the mutation.
Figure 1 on the left shows the predicted score ("digzyme score") calculated by digzyme and the experimental values. The Pearson correlation coefficient was 0.87. This result is slightly better than the existing popular physics-based method, FoldX (Figure 1 on the right).
Another physics-based method was used by the Pal Lab group, which employed a molecular dynamics (MD)-based approach for prediction. In this method, structural sampling (1 ns) is performed using MD, and the sampled structures are clustered into folded and unfolded states. Subsequently, energy calculations are performed for each representative structure in the clusters, and the values from equation (1) are calculated. By running this calculation for both the wild type and mutant, values can be obtained that can be compared with experimental data using equation (2). However, the assumption that the protein in the folded state (MD starting structure) will undergo a structural transition to the unfolded state within 1 ns under the given calculation conditions (27°C, typical equilibrium MD) is clearly unrealistic. This is because even for fast-folding proteins, which fold/unfold relatively quickly, simulations near their Tm still take over 1,000 times longer for a structural transition to occurr[3], the moderate correlation found using this method (Figure 1 on the right) is arguably a result of chance.
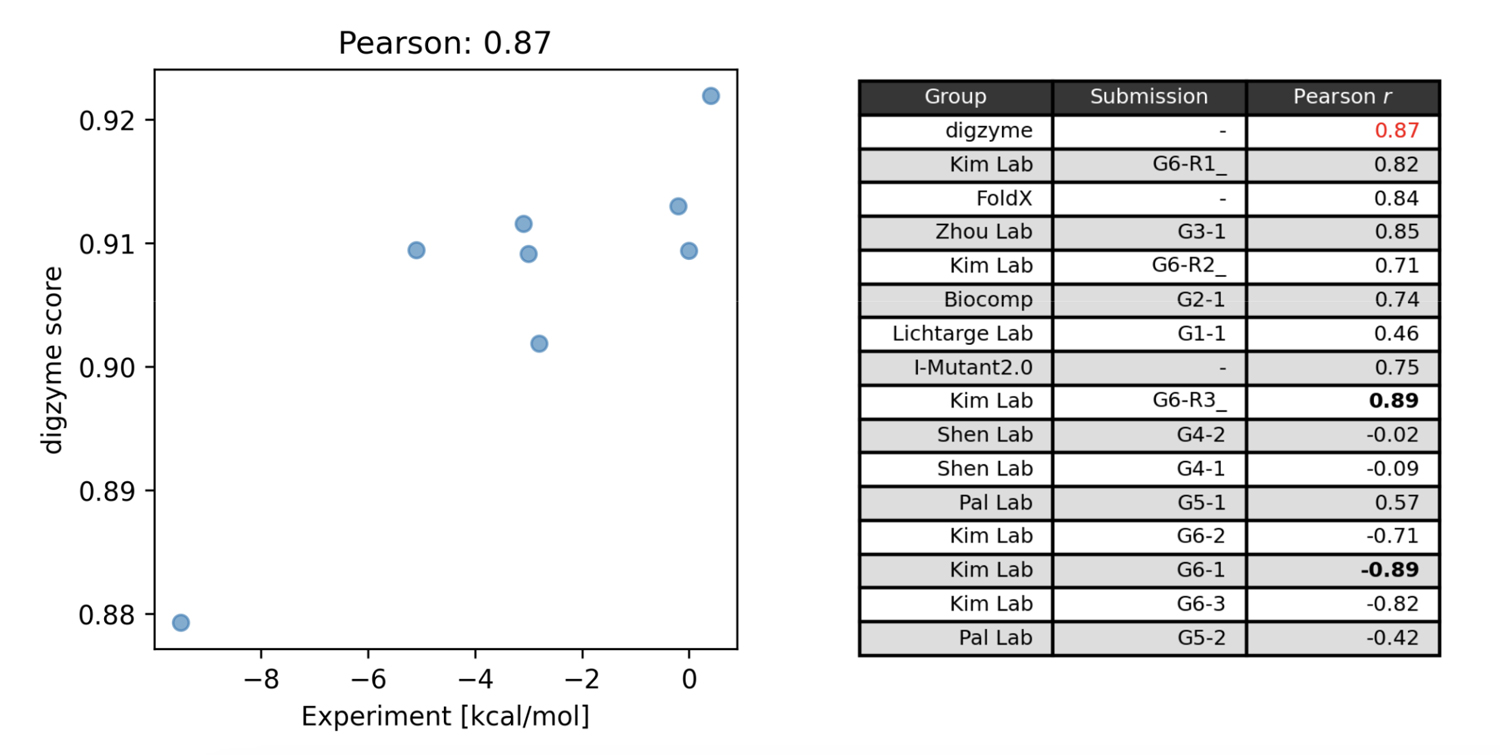
The group that proposed the model with the highest correlation in the contest was the Kim Lab group, with an absolute correlation coefficient of 0.89 (Figure 1, right). This group used a machine learning model for predictions, utilizing thermal stability data of mutants registered in the Protherm database for training [4]. In this machine learning model, both structure-based and amino acid sequence-based features are calculated, and a regression model is built using gradient boosting trees with these features. Among the structure-based features, the calculated values from the physical model FoldX are included, and it is known that these values are the most important features [4]. This fact suggests that using the digzyme score, a physical model with similar accuracy to that of FoldX, could help build even more advanced machine learning models. If there is a large amount of mutant data available for the target enzyme, it may be worth attempting to build a dedicated model.
Case 2. Prediction of Thermal Stability of Enzymes with the Same Function
In the search for useful enzymes, a large number of amino acid sequences of enzymes with the same (predicted) function are extracted from a database (forming the population), and candidate enzymes are selected by ranking them based on some criteria. Similar to mutant design, thermal stability is one of the important indicators in this process.
It is important to note that the prediction of thermal stability here is different from the prediction of the difference between wild-type and mutant enzymes as seen in Case 1. Typically, the length of the amino acid sequence is the same for both wild-type and mutant enzymes, and the sequence identity is often close to 99%. In contrast, in a population of sequences extracted from a database for a specific function, the length of the amino acid sequences varies, and the sequence identity is generally low. Predicting thermal stability and creating a ranking of sequences in such a population can often be challenging, as shown below.
The example here is a large-scale dataset of the Tm (melting temperature) of nanobodies (small fragments of antibodies) called NanoMelt, which was posted on a preprint server in September 2024[5]. This dataset includes both existing data and newly measured data by the authors (640 data points), with experimental conditions such as protein concentration, pH, and buffer standardized. For this dataset, the digzyme score was calculated for each enzyme using the same physical model as in Case 1, and the correlation with experimental values was examined.
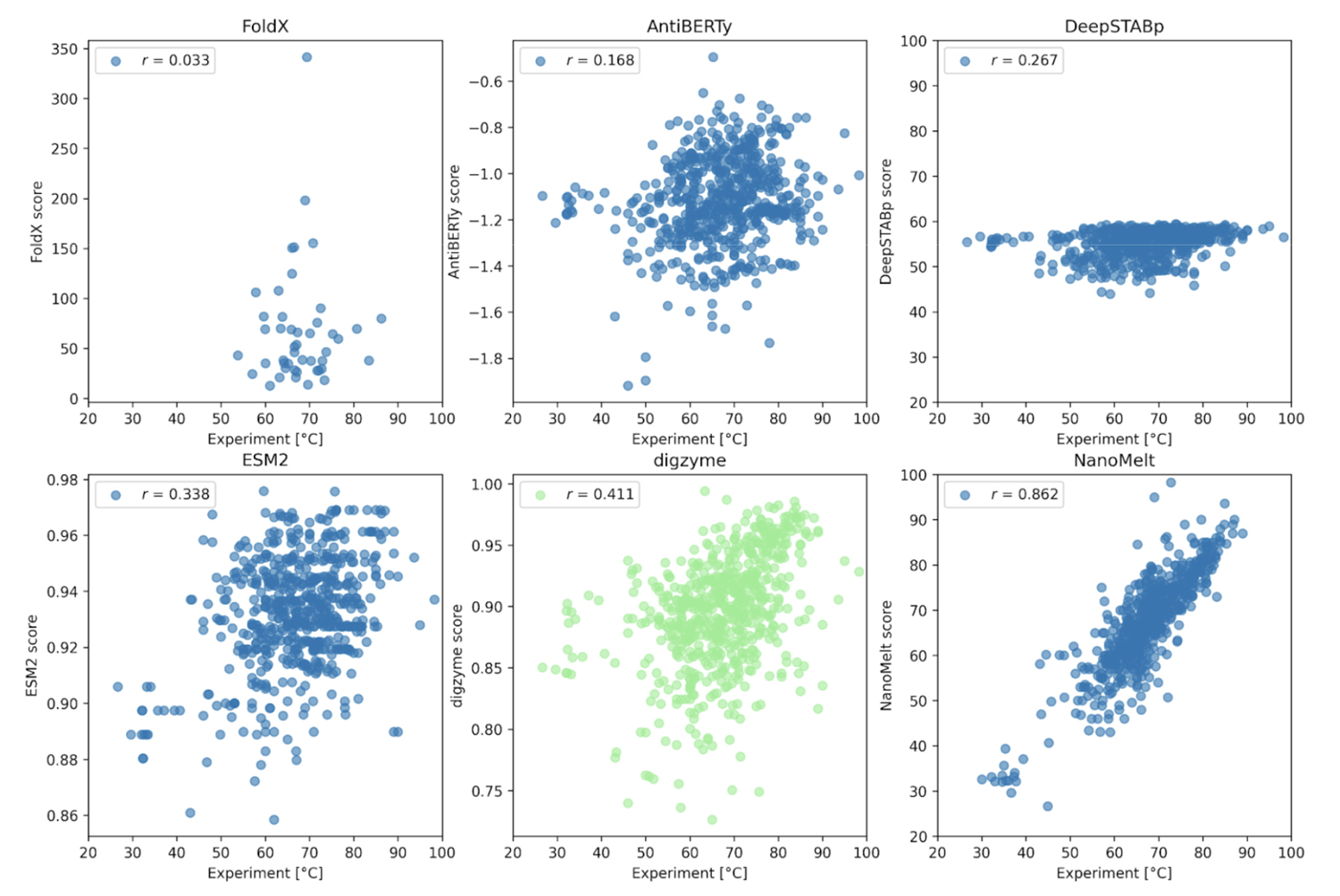
As shown in Figure 2, except for the results where the NanoMelt dataset itself was used for training (Figure 2, lower right), there was no or only weak correlation between the experimental values and the prediction results. First, FoldX, a physical model that achieved a high correlation coefficient in Case 1, failed to provide a correlated prediction result here. In contrast, digzyme successfully predicted a weakly correlated result (r = 0.411, Figure 2, lower center). Even when limiting the data to the 46 amino acid sequences used in FoldX predictions, a weak correlation was observed (r = 0.273), which signifies a remarkable advancement in expanding the applicability of existing physical models. AntiBERTy and ESM-2 are protein language models, and the scores in Figure 2 represent the (pseudo) log-likelihood of the amino acid sequences [5]. This is an indicator of the sequence's probability or plausiblity, and some correlation with thermal stability was expected. However, the actual correlation was weak (correlation coefficients of 0.168 and 0.338, respectively). Therefore, as the authors suggest, if these language models are used for thermal stability prediction, it would be better to build a model specialized for the task through further training [5]. On the other hand, the low correlation of DeepSTABp, a dedicated regression model for predicting Tm (r =0.267, Figure 2, upper right), requires careful consideration. According to the original paper [6], the Pearson correlation coefficient for DeepSTABp's test data was 0.90, yielding significant results. Despite this, the low correlation with the NanoMelt dataset suggests that this model may have overfitted and has limitations in generalization ability (i.e., it is powerless against "unfamiliar data"). In contrast, the physical model adopted by digzyme is based on general physical principles, which have no inherent limits to the range of amino acid sequences they can be applied to. In fact, since digzyme's model gives a higher correlation than DeepSTABp, it can be said that the superiority of the physical model is demonstrated to some extent.
Now, the NanoMelt model, which shows a strong correlation (r = 0.862, Figure 2, lower right), raises concerns about potential overfitting. Unfortunately, since NanoMelt is a nanobody-specific model, it is difficult to re-evaluate its performance on other datasets containing arbitrary protein sequences. Therefore, the authors selected six new sequences from the camel nanobody sequence database and experimentally measured Tm to re-evaluate the model. The criteria for selecting the sequences were as follows:
1.The dissimilarity with the most similar sequence in the NanoMelt dataset is at least 30%.
2.The AbNatiV VHH-nativeness score (a measure of sequence likelihood) is 0.85 or higher.
3.The predicted Tm in NanoMelt is either low (Tm < 61°C) or high (Tm > 73°C).
Of these six sequences, the three predicted to have low Tm did not express, but the three predicted to have high Tm did express, and successful Tm measurements were made. The error in the predicted results was approximately 1°C, demonstrating the high predictive performance of NanoMelt [5]. While this result does not definitively determine the presence of overfitting, it provides a clue to understanding the applicable range of the NanoMelt model.
Conclusion
In the context of enzyme discovery and modification, calculating the thermal stability of enzymes and creating an accurate ranking is crucial to reducing subsequent experimental processes. At digzyme, we tackle this challenge by applying a general-purpose physical model. In this blog, we evaluated our developed model by calculating prediction scores for two datasets. As shown in Case 1, we demonstrated that our model achieves practical accuracy in predicting the thermal stability of variants. However, as shown in Case 2, while we showed the superiority of our model over existing physical and machine learning models in comparing arbitrary amino acid sequences, the correlation with experimental values was weak, indicating room for further improvement.
Recently, there have been increasing successful cases of enzyme design using AI, with expectations for realizing novel folds (structures) and functions that were overlooked during the evolutionary process. However, the novelty of these designs makes predictions of physical properties, such as thermal stability, by machine learning challenging. Therefore, the importance of general-purpose physical models, such as those introduced in this blog, is expected to grow even more. At digzyme, we plan to continue actively advancing research and development to build more accurate and reliable models.
References
[1] CAGI5 Frataxin [Link]
[2] Savojardo et al. Hum. Mutat., 2019, 40(9), 1392 [Link]
[3] Lindorff-Larsen et al. Science, 2011, 334, 517 [Link]
[4] Berliner et al. PLoS ONE, 2014, 9(9), e107353 [Link]
[5] Ramon et al. bioRxiv, 2024 [Link]
[6] Jung et al. Int. J. Mol. Sci., 2023, 24(8), 7444 [Link]



